碁石無作為抽出例
碁石を無作為に抽出する例として、白を5個、黒を1個を袋に入れて、無作為に1個を取り出し、黒か白の確率を実際に行うととする。
1分間に10回繰り返せるとすれば、10分間で100回、20分間で200回繰り返せると期待できる。
学校教育関係者ではないので、実際にどれだけの時間を授業中に割けるかは知り得ません。仮に20分間実際に確率を確認するために実行できたとすると、Pythonプログラムでシミュレートした結果がこれです。
白:5個、黒:1個、試行回数:200、X軸の目盛数を10,Y軸の目盛数を10で実行
C:\Temp>python GoishiGraph2.py 5 1 200 10 10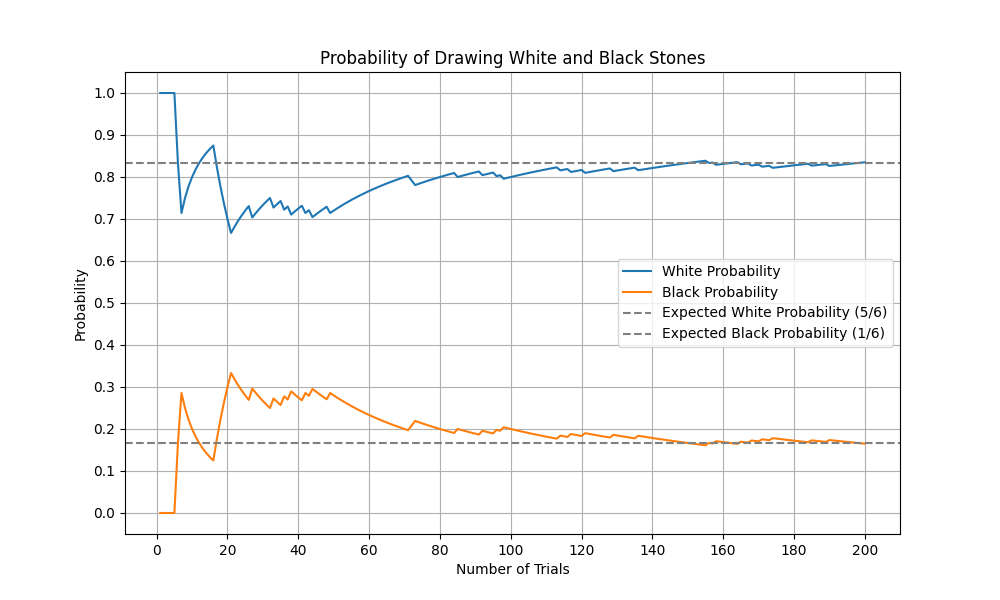
ですが、試行回数を5,000回にしてみると2,000回くらいが理論値に近いかと思われますが、10,000回以上は必要なようだ。
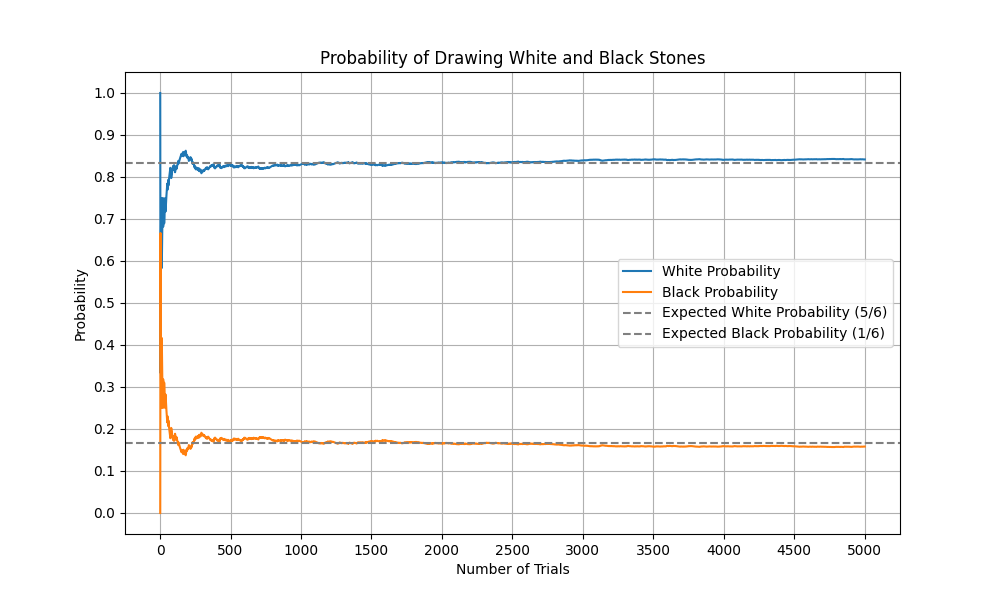
試行回数を20,000回で実行した場合、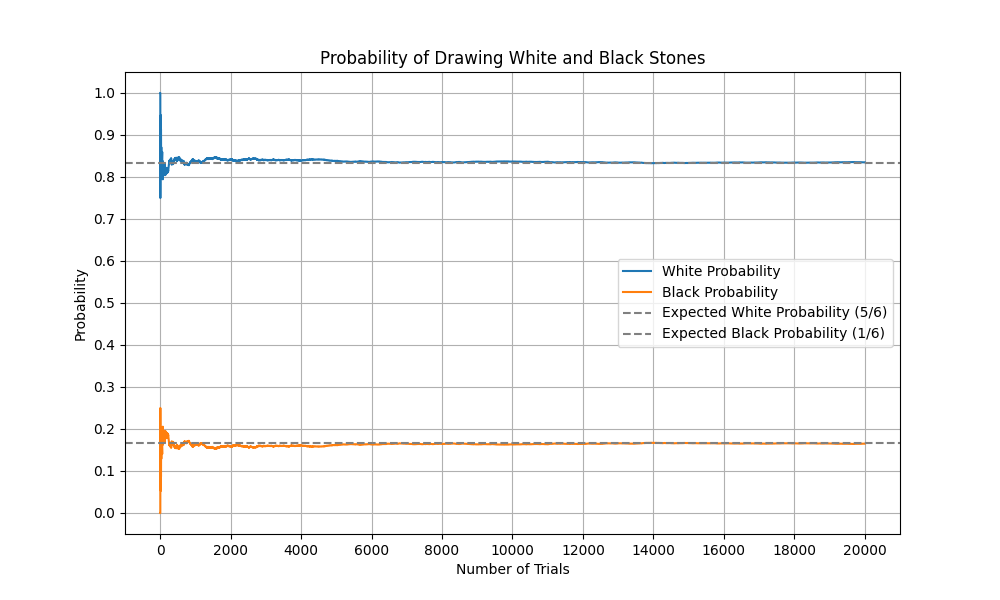
10,000回以上も試行しようとすると1,000分(16時間40分)かかりそうですら、実際に実行するのは困難と云えます。そこまでしなくても理論値に近づけるにはかなりの回数をしないことはわかるはずです。試行回数が少なければ、理論値から離れているので、どなたでも(中学生どころか小学生でも)わかるはずです。試行回数が少なくても大数の法則は理解されると判断できます。1,000回以上であっても100分以上試行する事となり、非現実的な行為となります。(根性論でやるべきことではない。いまは、令和です。昭和ではありません)
白と黒の組み合わせを変えてみる。
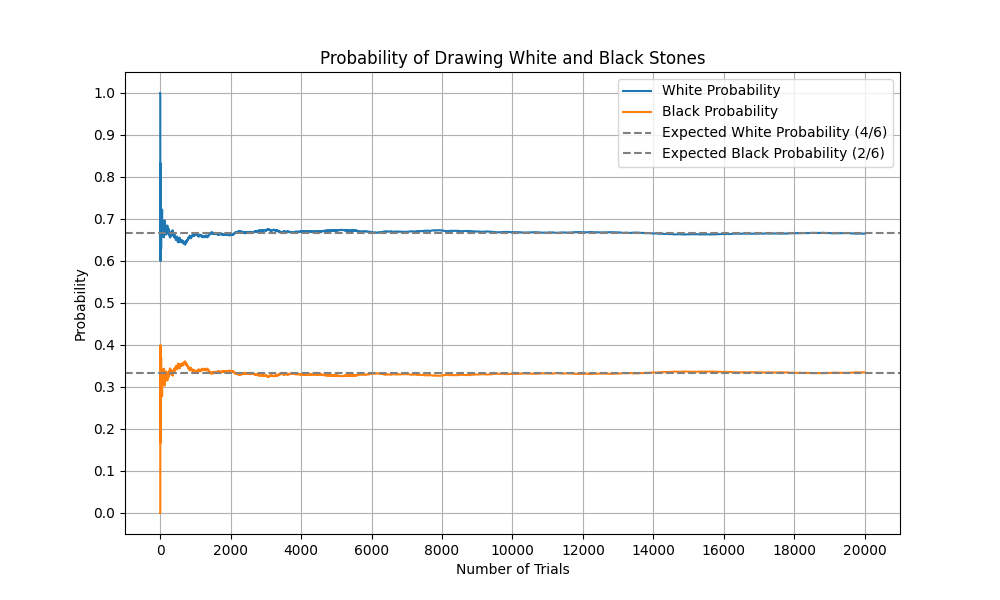
白:4個、黒:2個、試行回数:200、X軸の目盛数を10,Y軸の目盛数を10で実行
C:\Temp>python GoishiGraph2.py 4 2 200 10 10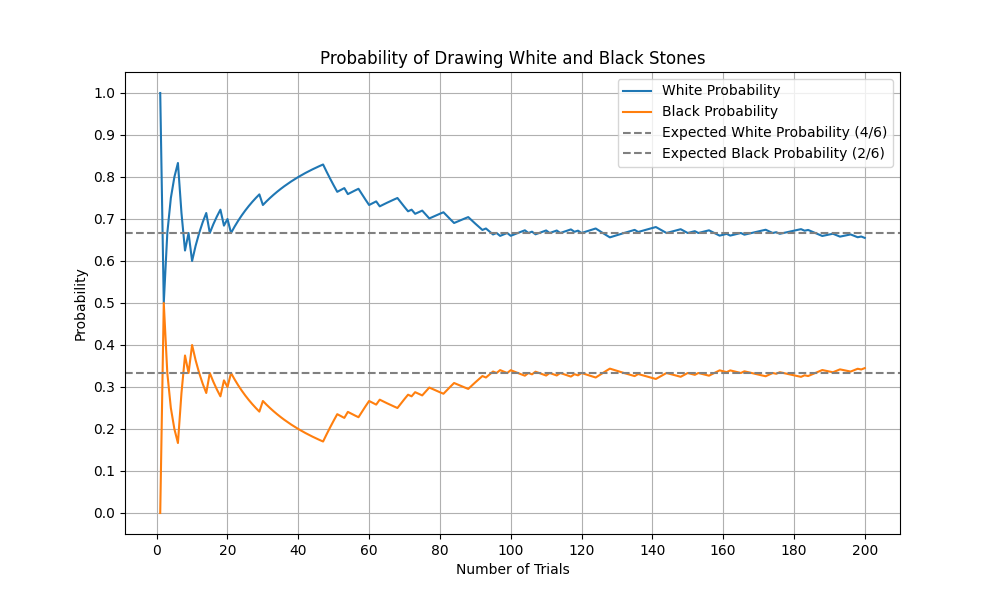
試行回数を20,000回で実行した場合、
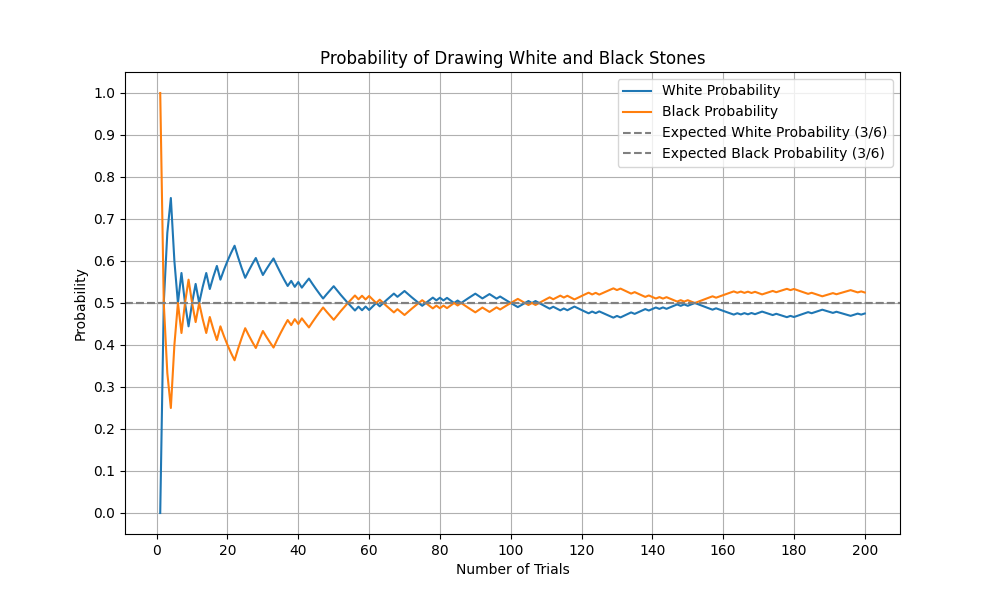
白:3個、黒:3個、試行回数:200、X軸の目盛数を10,Y軸の目盛数を10で実行
C:\Temp>python GoishiGraph2.py 3 3 200 10 10
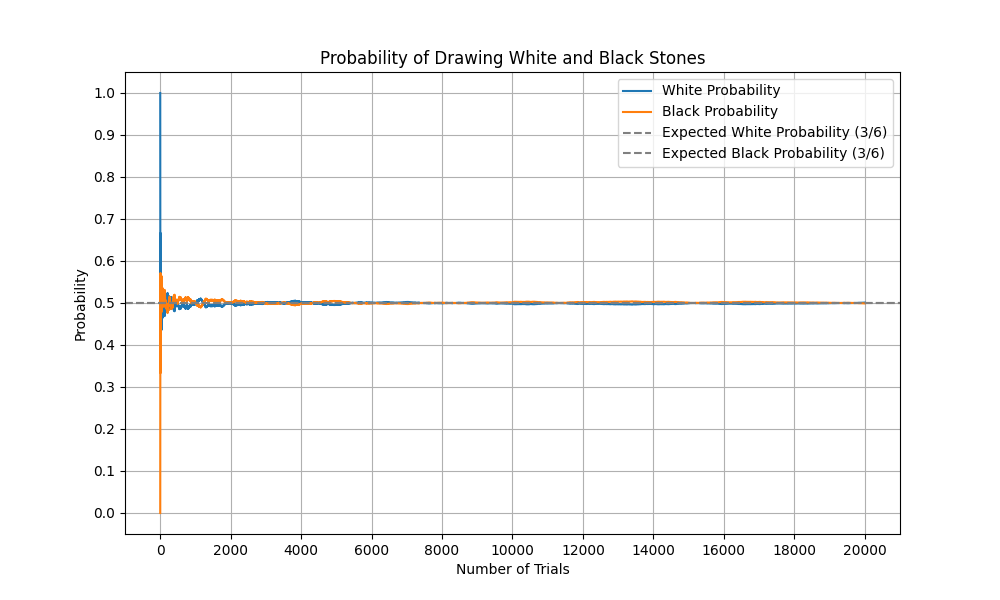
試行回数を20,000回で実行した場合、
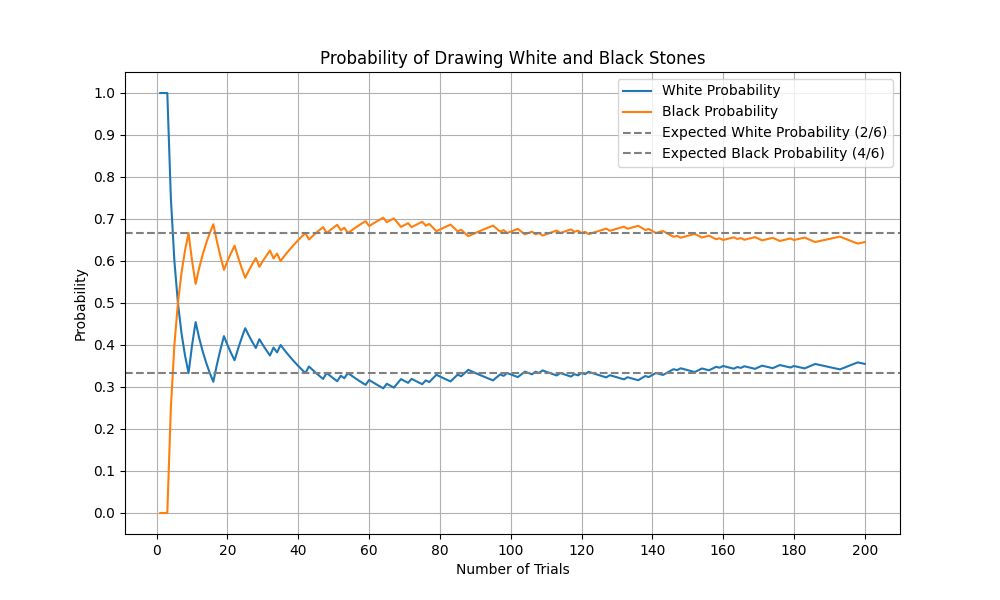
白:2個、黒:4個、試行回数:200、X軸の目盛数を10,Y軸の目盛数を10で実行
C:\Temp>python GoishiGraph2.py 2 4 200 10 10
試行回数を20,000回で実行した場合、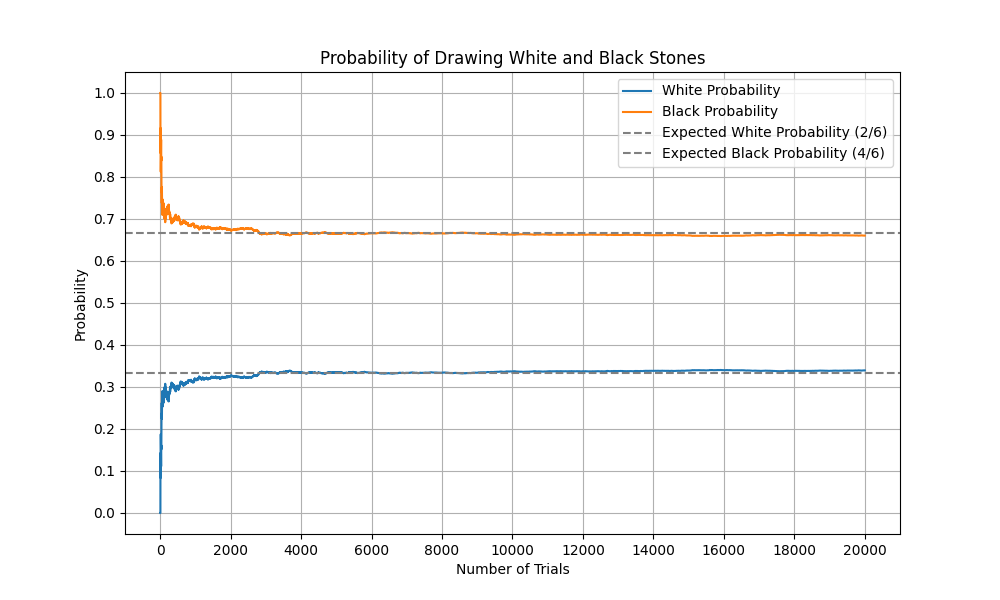
白:1個、黒:5個、試行回数:200、X軸の目盛数を10,Y軸の目盛数を10で実行
C:\Temp>python GoishiGraph2.py 1 5 200 10 10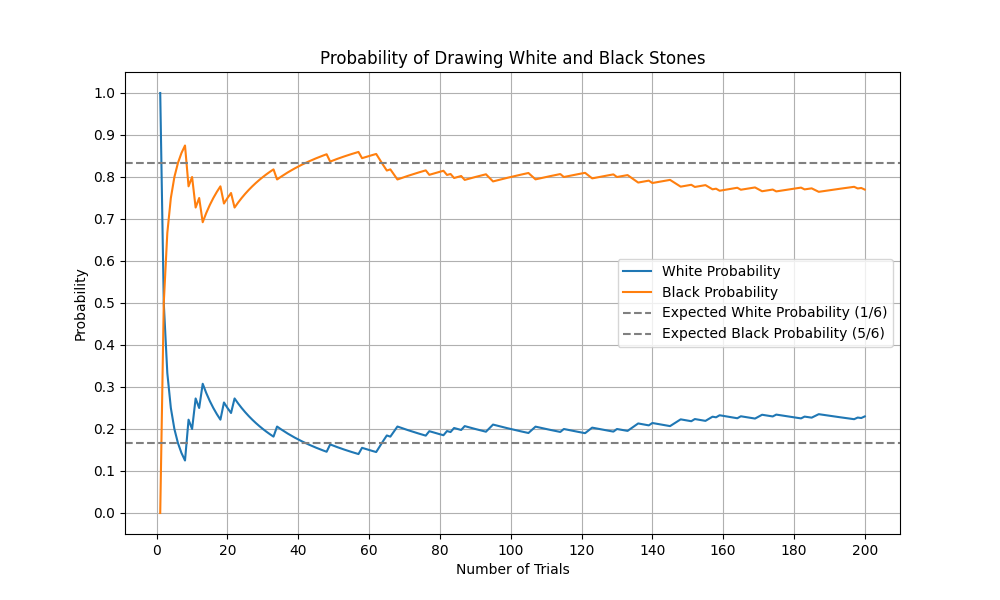
試行回数を20,000回で実行した場合、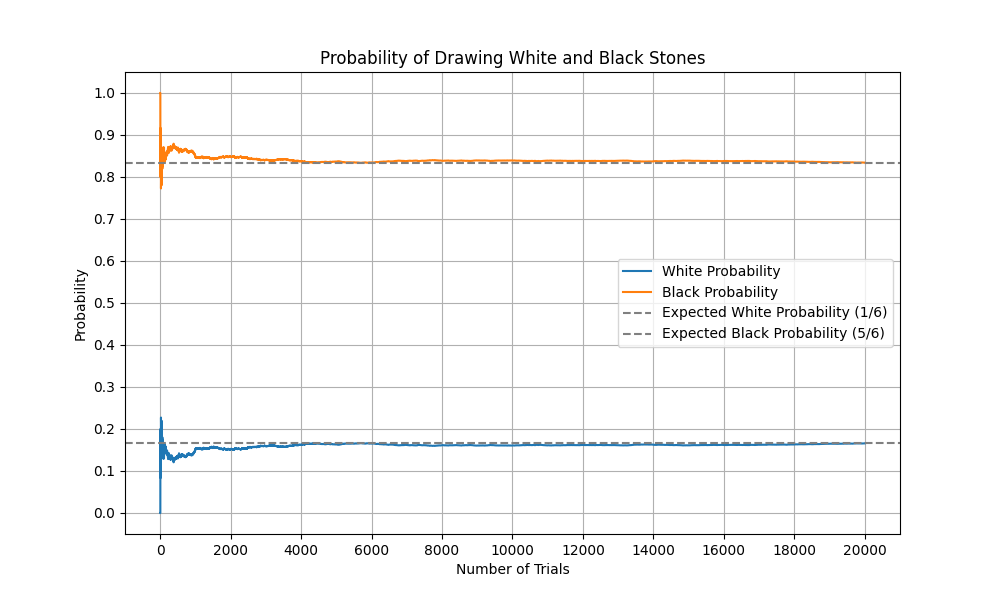
ソースコードはこちら GoiShiGraph2.py
